![]()
📚 Top 20 GCSE Maths Formulae You Must Memorize 📚
Hey there, students, parents, tutors, and teachers! 👋
Are you ready to conquer the GCSE Maths exams? 🏆 Here’s a handy guide to the top 20 formulae you simply can’t afford to forget!
1. Quadratic Formula 📈
The Quadratic Formula (x = -b ± √(b² – 4ac) / 2a) is a lifesaver when solving quadratic equations. Practice solving different types of quadratic equations to get comfortable with this formula.
2. Pythagorean Theorem ⚫️🟦🟦
In right-angled triangles, the square of the hypotenuse (c) is equal to the sum of the squares of the other two sides (a and b): c² = a² + b²
3. Trigonometric Identities ⚫️🟦🟦
Don’t forget these trigonometric identities:
- sin²(x) + cos²(x) = 1
- tan(x) = sin(x) / cos(x)
- cot(x) = 1 / tan(x)
- sec(x) = 1 / cos(x)
- cosec(x) = 1 / sin(x)
4. Binary Operations 💻
Understand the order of operations (BODMAS/BIDMAS/PEDMAS) to ensure your calculations are correct: Brackets, Orders (exponents and indices), Division and Multiplication (from left to right), Addition and Subtraction (from left to right)
5. Percentage Calculations 💼
Percentage calculations are essential for real-world problems. Remember these formulas:
- Percentage of a number = (part / whole) x 100%
- Increase/Decrease amount = (amount x percentage / 100)
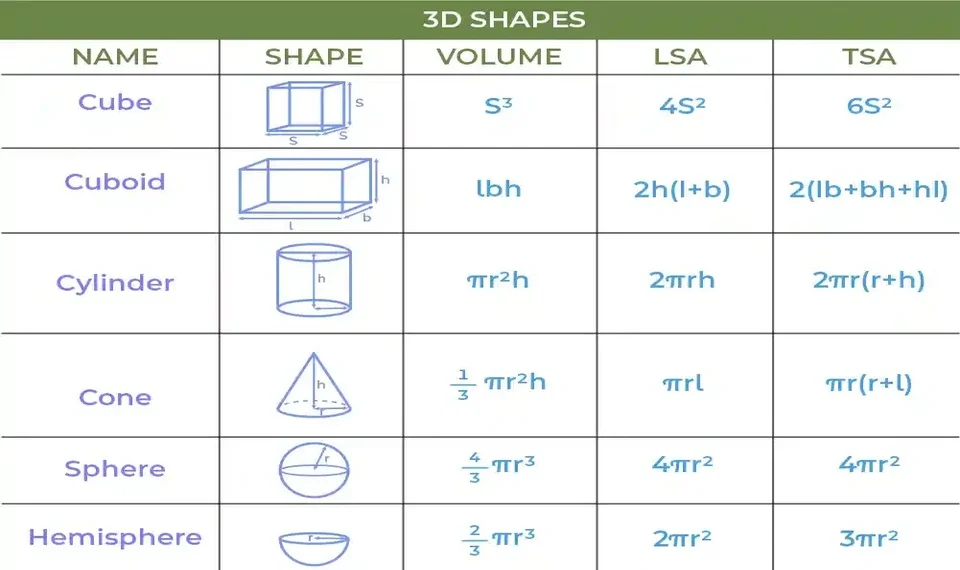
6. Areas and Volumes 🏠
Familiarize yourself with formulas for areas and volumes:
- Area of a rectangle = length x width
- Area of a triangle = 1/2 base x height
- Area of a circle = πr²
- Volume of a cube = side³
- Volume of a cylinder = πr²h
7. Probability 🎲
Understand probability concepts like:
- Total outcomes = events (S)
- Probability of an event = number of favourable outcomes / total outcomes
8. Coordinate Geometry 🌐
Don’t forget these coordinate geometry formulas:
- Distance between two points = √((x₂-x₁)² + (y₂-y₁)²)
- Midpoint of a line segment = [(x₁ + x₂) / 2, (y₁ + y₂) / 2]
9. Roots and Indices 🌱
Know the properties of roots and indices:
- a³ = a x a x a
- √(a³) = a
- a⁴ = a² x a²
- √(a⁴) = 2a²
10. Straight-Line Graphs 📈
For a straight-line graph, the gradient (m) = y₂ – y₁ / x₂ – x₁
11. Circle Theorems 🌐
Remember these circle theorems:
- Chord theorem: length of a chord = 2r ∫ (1 – cos(θ)) dθ
- Inradius theorem: length of the inradius = r ∫ (1 – cos(θ)) dθ
- Circumradius theorem: length of the circumradius = r ∫ (1 + cos(θ)) dθ
12. Logarithmic Formulas 💡
Get to grips with logarithmic formulas:
- logₐ(a) = x ⇔ a⁺x = 1
- aⁱ = 10^x
- log₁₀(a) = logₕ(a)
- logₗ(a) = (logₕ(a)) / logₕ(z)
13. Exponential Growth and Decay 🌱
Exponential growth and decay formulas are crucial for understanding real-world situations:
- A = A₀(1 + r)²t (exponential growth)
- A = A₀(1 – r)²t (exponential decay)
14. Differentiation 📈
Differentiation involves finding the rate of change of a function:
- d/dx (x²) = 2x
- d/dx (e^x) = e^x
- d/dx (ln(x)) = 1/x
15. Integration ⬆️
Integration helps you find the area under a curve:
- ∫x² dx = (1/3)x³ + C
- ∫e^xdx = e^x + C
- ∫ln(x) dx = xln(x) – x + C
16. Sequences and Series 📊
Sequences and series are essential for understanding patterns in numbers:
- Arithmetic sequence: aₙ = a₀ + (n-1)d
- Geometric sequence: aₙ = a₀r(n-1)
- Arithmetic series: Sₙ = (n/2)(a₁ + aₙ)
- Geometric series: Sₙ = a₀(1 – rⁱ)/(1 – r)
17. Binomial Theorem ⚫️🟦🟦
The binomial theorem helps in expanding binomials:
(a + b)ⁿ = ∑ (n choose k) * aⁿ-k * bⁿ-k, where n choose k = n! / (k! * (n-k)!)
18. Complex Numbers 🌈
Complex numbers involve real and imaginary parts:
- a + bi = ρ(cos(θ) + i sin(θ))
- ρ = √(a² + b²)
- θ = tan⁻¹(b/a)
19. Vectors 📐
Vectors are essential for solving problems involving displacement, forces, and velocities:
- Vector addition: a + b = (a₁ + b₁, a₂ + b₂)
- Scalar multiplication: ka = (ka₁, ka₂)
- Dot product: a . b = a₁b₁ + a₂b₂
- Cross product: a × b = (a₂b₃ – a₃b₂, a₃b₁ – a₁b₃, a₁b₂ – a₂b₁)
20. Matrices 📈
Matrices are used to represent systems of linear equations:
- Addition: A + B = (a₁₁ + b₁₁, a₁₂ + b₁₂, …)
- Multiplication: AB = (∑ a₁b₁j, ∑ a₂b₂j, …)
- Determinant of a 2×2 matrix: |A| = a₁₁a₂₂ – a₁₂a₂₁
FAQs ❓
💻 What’s the best way to remember all these formulae?
📝 Using mnemonics, flashcards, and practice problems can help solidify these formulae in your memory. Regular revision and practice is key to mastering them.
📖 Are these formulae only useful for GCSE Maths exams?
🌐 No, many of these formulae are fundamental to Maths and have applications in further studies, such as A-Level Maths, Science, Engineering, and beyond.
🎓 Can I use these formulae in real-life situations?
🌈 Absolutely! These formulae are essential for understanding and solving problems in many areas, including finance, physics, engineering, and everyday life.
📝 Are there any online resources for more practice problems?
🌐 Yes! Tutor GP offers online GCSE Maths Tuition, where you can find plenty of practice problems and expert tutoring to help you master these formulae.
👨🏫 Are tutors available to help with understanding these formulae?
👩🏫 Definitely! Tutor GP provides personalised online tuition for GCSE Maths, Science, and A-Level Physics, among other subjects.
📅 When should I start learning these formulae?
🕰️ Ideally, you should start learning these formulae as early as possible. However, it’s never too late to start – even in the weeks leading up to the exams.
🧠 Are there any apps or tools to help me memorize these formulae?
📱 Yes, there are many educational apps and tools available that can help you learn and memorize these formulae effectively. Spaced repetition apps, such as Anki or Quizlet, are particularly useful.